Golden Spiral
In geometry, a Golden Spiral is a logarithmic spiral whose growth factor is φ, the Golden Ratio. That is, a golden spiral gets wider (or further from its origin) by a factor of φ 1.618 for every quarter turn it makes.[1]
Approximations of the golden spiral
There are several similar spirals that approximate, but do not exactly equal, a golden spiral. These are often confused with the golden spiral.
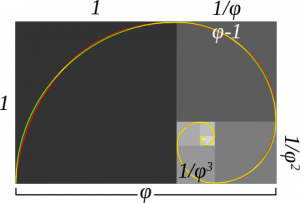
For example, a golden spiral can be approximated by first starting with a rectangle for which the ratio between its length and width is the Golden Ratio. This rectangle can then be partitioned into a square and a similar rectangle and the rectangle can then be split in the same way. After continuing this process for an arbitrary amount of steps, the result will be an almost complete partitioning of the rectangle into squares. The corners of these squares can be connected by quarter-circles. The result, though not a true logarithmic spiral, approximates a golden spiral.
Another approximation is a Fibonacci spiral, which is constructed similarly to the above method except that you start with a rectangle partitioned into 2 squares and then in each step add to the rectangle's longest side a square of the same length. Since the ratio between consecutive Fibonacci numbers approaches the Golden Ratio as the Fibonacci numbers approach infinity, so too does this spiral get more similar to the previous approximation the more squares are added.
HGS Reference
Correct Calculus, Mathematical Code, Page 80

