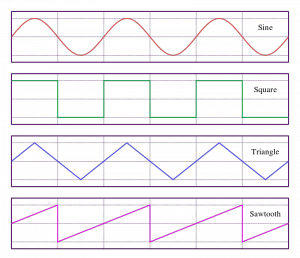
Sine Wave
The Sine Wave or sinusoid is a mathematical curve that describes a smooth repetitive Oscillation. It is named after the function sine, of which it is the graph. It occurs often in pure and applied mathematics, as well as physics, engineering, signal processing and many other fields. The sine wave is important in physics because it retains its wave shape when added to another sine wave of the same Frequency and arbitrary phase and magnitude. It is the only periodic waveform that has this property. This property leads to its importance in Fourier analysis and makes it acoustically unique. This wave pattern occurs often in nature, including ocean waves, sound waves, and light waves.Since sine waves propagate without changing form in distributed linear systems, they are often used to analyze wave propagation.
When two waves having the same amplitude and frequency, and traveling in opposite directions, superpose each other, then a standing wave pattern is created. Note that, on a plucked string, the interfering waves are the waves reflected from the fixed end points of the string. Therefore, standing waves occur only at certain frequencies, which are referred to as resonant frequencies and are composed of a fundamental frequency and its higher harmonics. The resonant frequencies of a string are determined by the length between the fixed ends and the tension of the string.
The human ear can recognize single sine waves as sounding clear because sine waves are representations of a single frequency with no harmonics; some sounds that approximate a pure sine wave are whistling, a crystal glass set to vibrate by running a wet finger around its rim, and the sound made by a tuning fork. To the human ear, a sound that is made of more than one sine wave will have perceptible harmonics; addition of different sine waves results in a different waveform and thus changes the timbre of the sound.
Fourier series
In 1822, French mathematician Joseph Fourier discovered that sinusoidal waves can be used as simple building blocks to describe and approximate any periodic waveform, including square waves. Fourier used it as an analytical tool in the study of waves and heat flow. It is frequently used in signal processing and the statistical analysis of time series. [1]

