Golden Ratio

Golden Ratio

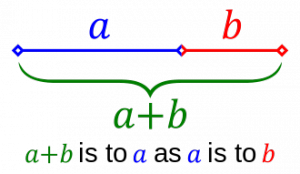
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. The figure on the right illustrates the geometric relationship. Fibonacci spirals, Golden spirals and Golden Ratio based spirals often appear in living organisms. The Golden Ratio is also found in geometry, appearing in basic constructions of an equilateral triangle, square and pentagon placed inside a circle, as well as in more complex three-dimensional solids such as dodecahedrons, icosahedrons and Buckyballs.

Phi is also used as a symbol for the Golden Ratio and on other occasions in math and science. This use is separately encoded as the Unicode glyph ϕ.

The Golden Ratio 1.618033988749894848204586834... in mathematics, art, and architecture.

The Golden Ratio also is called the golden mean or golden section. Other names include extreme and mean ratio, medial section, divine proportion, divine section , golden proportion, golden cut, and golden number.

Plato (427–347 BC), in his Timaeus, describes five possible regular solids (the Platonic Solids: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron), some of which are related to the Golden Ratio.

The term "Phi" was coined by American mathematician Mark Barr in the 1900s. Phi has continued to appear in mathematics and physics, including the 1970s Penrose Tiles, which allowed surfaces to be tiled in five-fold symmetry. In the 1980s, phi appeared in quasi crystals, a then-newly discovered form of matter.

Golden Ratio in Renaissance Art

The drawing is based on the correlations of ideal human proportions with geometry described by the ancient Roman architect Vitruvius in Book III of his treatise De Architectura.

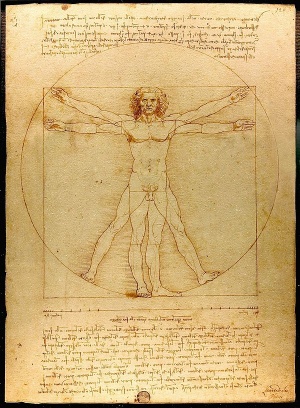
In 1509, Luca Pacioli wrote a book that refers to the number as the "Divine Proportion," which was illustrated by Leonardo da Vinci. Da Vinci later called this sectio aurea or the Golden section. The Golden ratio was used to achieve balance and beauty in many Renaissance paintings and sculptures. Da Vinci himself used the Golden ratio to define all of the proportions in his Last Supper, including the dimensions of the table and the proportions of the walls and backgrounds. The Golden ratio also appears in da Vinci's Vitruvian Man and the Mona Lisa. Other artists who employed the Golden ratio include Michelangelo, Raphael, Rembrandt, Seurat, and Salvador Dali.

The Vitruvian Man, is a drawing by Leonardo da Vinci around 1490. It is accompanied by notes based on the work of the architect Vitruvius. The drawing, which is in pen and ink on paper, depicts a man in two superimposed positions with his arms and legs apart and inscribed in a circle and square. The drawing and text are sometimes called the Canon of Proportions or, less often, Proportions of Man.

Golden Ratio in Nature

The Golden ratio also appears in all forms of nature and science. Some places include:

• Flower petals: The number of petals on some flowers follows the Fibonacci sequence.
• Seed heads: The seeds of a flower are often produced at the center and migrate outward to fill the space. For example, sunflowers follow this pattern.
• Pinecones: The spiral pattern of the seed pods spiral upward in opposite directions. The number of steps the spirals take tend to match Fibonacci numbers.
• Sunflower seeds: Sunflower seeds grow in Fibonacci spirals.
• Tree branches: The way tree branches form or split is an example of the Fibonacci sequence. Root systems and algae exhibit this formation pattern.
• Shells: Many shells, including snail shells and nautilus shells, are perfect examples of the Golden spiral.
• Spiral galaxies: The Milky Way has a number of spiral arms, each of which has a logarithmic spiral of roughly 12 degrees. The shape of the spiral is identical to the Golden spiral, and the Golden rectangle can be drawn over any spiral galaxy.
• Hurricanes: Much like shells, hurricanes often display the Golden spiral.
• Fingers: The length of our fingers, each section from the tip of the base to the wrist is larger than the preceding one by roughly the ratio of phi.
• Animal bodies: The measurement of the human navel to the floor and the top of the head to the navel is the Golden ratio. But we are not the only examples of the Golden ratio in the animal kingdom; dolphins, starfish, sand dollars, sea urchins, ants and honeybees also exhibit the proportion.
• DNA molecules: A DNA molecule measures 34 angstroms by 21 angstroms at each full cycle of the double helix spiral. In the Fibonacci series, 34 and 21 are successive numbers.

Fibonacci Spiral

The Fibonacci spiral gets closer and closer to a Golden Spiral as it increases in size because of the ratio of each number in the Fibonacci series to the one before it converges on Phi, 1.618, as the series progresses. Beginning with Zero, then 1, it then moves on to the next number, as such : 0+1=1, 1+1=2, 2+1=3, 3+2=5, 5+3=8 and so forth. When we apply this mathematical formula to quantify or measure the movement of energy or Consciousness within time or space, the Fibonacci Spiral loses its connection going back to the Zero Point or Source, instead the sequence uses the previous number to add into itself to get to the next higher number of the sequence. The Fibonacci Spiral illustrates the math used to perpetuate the war over energy, therefore the consciousness suppression on the earth, as when the sequence grows in number or size, it is due to the consumption of the previous values in order to grow itself larger.The larger it gets, the more it progressively moves out and away from the Krystal Spiral of the original core manifestation body or divine template body, as it expands. (See Consumptive Modeling). Therefore the Fibonacci Spiral is a model of Metatronic Reversal in the consciousness fields that ultimately attach like a parasite to a living host, collecting waste products, such as accumulating toxic Miasma fields which form into the Qlippoth or Adverse Sephiroth, in the Phantom Matrix to infect the Universal Tree of Life.

HGS Reference

Correct Calculus, Mathematical Code, "Golden Ratio" Page 80

See Also

Sacred Geometry