Sonic Geometry: Difference between revisions
| (7 intermediate revisions by the same user not shown) | |||
| Line 14: | Line 14: | ||
==Triangle 180 Degrees== | ==Triangle 180 Degrees== | ||
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. An equilateral triangle has three sides of the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°. <ref>[https://en.wikipedia.org/wiki/Triangle Triangle wiki]</ref> | [[File:Regular polygon 3 annotated.svg|thumb|Equilateral triangle with annotation.]] | ||
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. An equilateral triangle has three sides of the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°. Triangles are assumed to be two-dimensional plane figures, unless the context provides otherwise. In rigorous treatments, a triangle is therefore called a 2-simplex (see also Polytope). Elementary facts about triangles were presented by Euclid, in books 1–4 of his Elements, written around 300 BC. | |||
The measures of the interior angles of the triangle always add up to 180 degrees (same color to point out they are equal). The sum of the measures of the interior angles of a triangle in Euclidean space is always 180 degrees. This fact is equivalent to Euclid's parallel postulate. This allows determination of the measure of the third angle of any triangle, given the measure of two angles. An exterior angle of a triangle is an angle that is a linear pair (and hence supplementary) to an interior angle. The measure of an exterior angle of a triangle is equal to the sum of the measures of the two interior angles that are not adjacent to it; this is the exterior angle theorem. The sum of the measures of the three exterior angles (one for each vertex) of any triangle is 360 degrees. | |||
<ref>[https://en.wikipedia.org/wiki/Triangle Triangle wiki]</ref> | |||
==Square 360 Degrees== | ==Square 360 Degrees== | ||
[[File:Regular polygon 4 annotated.svg|thumb|Square with annotation.]] | |||
In geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, or 100-gradian angles or right angles). It can also be defined as a rectangle in which two adjacent sides have equal length. | In geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, or 100-gradian angles or right angles). It can also be defined as a rectangle in which two adjacent sides have equal length. | ||
* Opposite sides of a square are both parallel and equal in length. | * Opposite sides of a square are both parallel and equal in length. | ||
| Line 24: | Line 30: | ||
==Pentagon 540 Degrees== | ==Pentagon 540 Degrees== | ||
[[File:Regular polygon 5 annotated.svg|thumb|Regular pentagon with annotation.]] | |||
In geometry, a pentagon (from the Greek πέντε pente and γωνία gonia, meaning five and angle) is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°. | In geometry, a pentagon (from the Greek πέντε pente and γωνία gonia, meaning five and angle) is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°. | ||
| Line 29: | Line 36: | ||
==Hexagon 720 Degrees== | ==Hexagon 720 Degrees== | ||
[[File:Regular polygon 6 annotated.svg|thumb|Hexagon|Regular hexagon with annotation.]] | |||
In geometry, a hexagon (from Greek ἕξ, hex, meaning "six", and γωνία, gonía, meaning "corner, angle") is a six-sided polygon or 6-gon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°. A regular hexagon has six rotational symmetries (rotational symmetry of order six) and six reflection symmetries (six lines of symmetry). <ref>[https://en.wikipedia.org/wiki/Hexagon Hexagon wiki]</ref> | In geometry, a hexagon (from Greek ἕξ, hex, meaning "six", and γωνία, gonía, meaning "corner, angle") is a six-sided polygon or 6-gon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°. A regular hexagon has six rotational symmetries (rotational symmetry of order six) and six reflection symmetries (six lines of symmetry). <ref>[https://en.wikipedia.org/wiki/Hexagon Hexagon wiki]</ref> | ||
| Line 36: | Line 44: | ||
The heptagon is sometimes referred to as the septagon, using "sept-" (an elision of septua-, a Latin-derived numerical prefix, rather than hepta-, a Greek-derived numerical prefix; both are cognate) together with the Greek suffix "-agon" meaning angle.<ref>[https://en.wikipedia.org/wiki/Heptagon Heptagon wiki]</ref> | The heptagon is sometimes referred to as the septagon, using "sept-" (an elision of septua-, a Latin-derived numerical prefix, rather than hepta-, a Greek-derived numerical prefix; both are cognate) together with the Greek suffix "-agon" meaning angle.<ref>[https://en.wikipedia.org/wiki/Heptagon Heptagon wiki]</ref> | ||
==Octagon 1080 Degrees== | |||
[[File:Regular polygon 8 annotated.svg|thumb|Regular octagon with annotation.]] | |||
In geometry, an octagon (from the Greek ὀκτάγωνον oktágōnon, "eight angles") is an eight-sided polygon or 8-gon.The sum of all the internal angles of any octagon is 1080°. As with all polygons, the external angles total 360°. | |||
If squares are constructed all internally or all externally on the sides of an octagon, then the midpoints of the segments connecting the centers of opposite squares form a quadrilateral that is both equidiagonal and orthodiagonal (that is, whose diagonals are equal in length and at right angles to each other). | |||
The midpoint octagon of a reference octagon has its eight vertices at the midpoints of the sides of the reference octagon. If squares are constructed all internally or all externally on the sides of the midpoint octagon, then the midpoints of the segments connecting the centers of opposite squares themselves form the vertices of a square.<ref>[https://en.wikipedia.org/wiki/Octagon Octagon wiki]</ref> | |||
==References== | ==References== | ||
Latest revision as of 00:31, 9 August 2021
When our planet was invaded, these nonhuman forces understood they would gain control over sound waves and sonic geometries in the architecture, if they destroyed the mother principle by disfiguring the sound body templates throughout the planetary network and then replaced it with an artificial version. Further they knew that to enslave a species, they could effectively use the power of sound waves and frequency along with dissonant geometric programs to trigger reversal stimuli that conditioned us to damage our own human DNA potential.
Yet we must learn from the sound wave weaponry and sonic geometric code programs that have been used against us and reclaim the power of sound technologies for the empowerment and upliftment of all humanity. All human beings are exceptionally receptive and inclined to reverberate with resonating sound tones or energy waves, especially those that naturally emanate from the planetary body. When we can utilize sound waves such as harmonious music, words or tones that feel positively resonant in the cells of our body, we automatically increase inner harmony and coherence, which greatly strengthens our spiritual and physical immunity.
Curiously, the beauty of the sonic geometries is increasingly present in the extensive fields of plasma flower activations happening in the planetary architecture as the result of the Return of Emerald Order. These naturally sing the frequencies of the Christos-Sophia twinned heart song which emphasizes the amazingly high frequency of flowers wherever they are found, which is inherent within the Holy Mother’s sound signature of the holy spirit’s sonic geometries. The frequency of flowers in their plasma architecture are reorganizing the energy field with high frequency geometric flower patterns of every shape and essence, highlighting the Sophianic power of sonic plasma flower shields that are now returning and healing the planetary grid to circulate chalice points of living light current.
To regain our minds and our health, we must regain the knowledge of the immense power behind sound technology and sonic geometries for spiritual healing through the science of Cymatics, and how this information was actually at the foundation of building the energy circulating architecture of our technologically advanced human society in which poverty and disease was nonexistent.
Earth and Platonic Solids
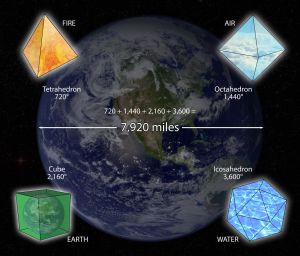
The sonic geometries, Light Symbol Codes are based in the platonic solid shapes and lines of light are programmed from one dimension above where they are being directly placed in the field. This is accomplished by directing geometric codes from mathematical shapes which form into light programs into one dimensional area in order to direct the appropriate sound frequencies into the dimension above it. In directing certain light code symbols into a specific dimension of time and space, the architect behind the making of the Blueprint is simultaneously directing sound wave frequencies or sonic geometries into the dimension that exists above it. Remember that sound makes geometric forms which become patterns made visible through light. The interplay of light and sound must be used together in the creation of energy fields and forms, and thus the male and female principle are always entwined and working together in some capacity in the mechanics of creation.[1]
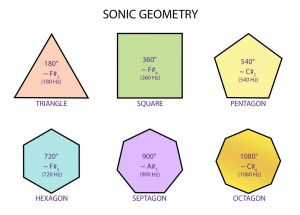
Triangle 180 Degrees

A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. An equilateral triangle has three sides of the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°. Triangles are assumed to be two-dimensional plane figures, unless the context provides otherwise. In rigorous treatments, a triangle is therefore called a 2-simplex (see also Polytope). Elementary facts about triangles were presented by Euclid, in books 1–4 of his Elements, written around 300 BC.
The measures of the interior angles of the triangle always add up to 180 degrees (same color to point out they are equal). The sum of the measures of the interior angles of a triangle in Euclidean space is always 180 degrees. This fact is equivalent to Euclid's parallel postulate. This allows determination of the measure of the third angle of any triangle, given the measure of two angles. An exterior angle of a triangle is an angle that is a linear pair (and hence supplementary) to an interior angle. The measure of an exterior angle of a triangle is equal to the sum of the measures of the two interior angles that are not adjacent to it; this is the exterior angle theorem. The sum of the measures of the three exterior angles (one for each vertex) of any triangle is 360 degrees. [2]
Square 360 Degrees

In geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, or 100-gradian angles or right angles). It can also be defined as a rectangle in which two adjacent sides have equal length.
- Opposite sides of a square are both parallel and equal in length.
- All four angles of a square are equal (each being 360°/4 = 90°, a right angle).
- All four sides of a square are equal.
- The diagonals of a square are equal.[3]
Pentagon 540 Degrees

In geometry, a pentagon (from the Greek πέντε pente and γωνία gonia, meaning five and angle) is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
A pentagon may be simple or self-intersecting. A self-intersecting regular pentagon (or star pentagon) is called a pentagram. A regular pentagon has five lines of reflectional symmetry, and rotational symmetry of order 5 (through 72°, 144°, 216° and 288°). The diagonals of a convex regular pentagon are in the golden ratio to its sides. [4]
Hexagon 720 Degrees

In geometry, a hexagon (from Greek ἕξ, hex, meaning "six", and γωνία, gonía, meaning "corner, angle") is a six-sided polygon or 6-gon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°. A regular hexagon has six rotational symmetries (rotational symmetry of order six) and six reflection symmetries (six lines of symmetry). [5]
Septagon 900 Degrees

Septagon A 7-sided polygon (a flat shape with straight sides). Also called Heptagon.In geometry, a heptagon is a seven-sided polygon or 7-gon.
The heptagon is sometimes referred to as the septagon, using "sept-" (an elision of septua-, a Latin-derived numerical prefix, rather than hepta-, a Greek-derived numerical prefix; both are cognate) together with the Greek suffix "-agon" meaning angle.[6]
Octagon 1080 Degrees

In geometry, an octagon (from the Greek ὀκτάγωνον oktágōnon, "eight angles") is an eight-sided polygon or 8-gon.The sum of all the internal angles of any octagon is 1080°. As with all polygons, the external angles total 360°.
If squares are constructed all internally or all externally on the sides of an octagon, then the midpoints of the segments connecting the centers of opposite squares form a quadrilateral that is both equidiagonal and orthodiagonal (that is, whose diagonals are equal in length and at right angles to each other).
The midpoint octagon of a reference octagon has its eight vertices at the midpoints of the sides of the reference octagon. If squares are constructed all internally or all externally on the sides of the midpoint octagon, then the midpoints of the segments connecting the centers of opposite squares themselves form the vertices of a square.[7]

